Bayes' theorem & Bayesian probability & Bayesian inference

先知道什麼是conditional probability 和 marginal probability

Conditional probability is the probability of some event A, given the occurrence of some other event B. Conditional probability is written P(A|B), and is read "the probability of A, given B".

Joint probability is the probability of two events in conjunction. That is, it is the probability of both events together. The joint probability of A and B is written 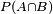or

Marginal probability is then the unconditional probability P(A) of the event A; that is, the probability of A, regardless of whether event B did or did not occur. If B can be thought of as the event of a random variable X having a given outcome, the marginal probability of A can be obtained by summing (or integrating, more generally) the joint probabilities over all outcomes for X. For example, if there are two possible outcomes for X with corresponding events B and B', this means that 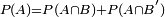. This is called marginalization.

Conditioning of probabilities, i.e. updating them to take account of (possibly new) information, may be achieved through Bayes' theorem. In such conditioning, the probability of A given only initial information I, P(A|I), is known as the prior probability. The updated conditional probability of A, given I and the outcome of the event B, is known as the posterior probability, P(A|B,I).

Simple statement of theorem

Bayes gave a special case involving continuous prior and posterior probability distributions and discrete probability distributions of data, but in its simplest setting involving only discrete distributions, Bayes' theorem relates the conditional and marginal probabilities of events A and B, where B has a non-vanishing probability:

.

Each term in Bayes' theorem has a conventional name:

• P(A) is the prior probability or marginal probability of A. It is "prior" in the sense that it does not take into account any information about B.
• P(A|B) is the conditional probability of A, given B. It is also called the posterior probability because it is derived from or depends upon the specified value of B.
• P(B|A) is the conditional probability of B given A.
• P(B) is the prior or marginal probability of B, and acts as a normalizing constant.

Bayes' theorem in this form gives a mathematical representation of how the conditional probabability of event A given B is related to the converse conditional probabablity of B given A.

Likelihood
in statistical usage there is a clear distinction: whereas "probability" allows us to predict unknown outcomes based on known parameters, "likelihood" allows us to estimate unknown parameters based on known outcomes.